

Rational numbers in decimal form always have a finite or repeating decimal expansion. On the other hand, the number pi (3.14159…) cannot be expressed as a fraction with integers for both the numerator and denominator. If not, then it is notrational.įor example, the number 3 can be expressed as 3/1, which is a fraction with an integer numerator and an integer denominator. To identify whether a given number is rational, you can check to see if it can be expressed as a fraction. The set of rational numbers includes all integers, since every integer can be written as a fraction with a denominator of 1. Rational numbers are any number that can be expressed as a fraction, where both the numerator and denominator are integers. So 0.5 would become 5/10 because there is one digit to the left of the original decimal point (0), and two digits total including zeroes (0 and 5). All decimals can be converted to fractions by moving the decimal point over until there is only one digit to the left of it, and counting how many digits there are total including zeroes on both sides of the original decimal point. For example, 0.5, 1.25, and 2.75 are all decimals. A decimal is simply a number with a decimal point somewhere within it. Therefore, the fraction 7/3 would be written as 2 1/3.ĭecimals are another form of rational number that can be easily converted to fractions. For example, if someone were to ask you to divide 7 by 3, the answer would be 2 with a remainder of 1 (2.333…). The quotient is the integer part of the fraction, while the remainder is the decimal part. They are created when one number is divided by another number, resulting in a quotient and a remainder. Another way is by their properties, such as being positive or negative, and whether or not they are prime numbers.įractions are the most common type of rational number. One way is by how they are represented, which include fractions, decimals, and percentages.

Rational numbers can be classified in different ways. Some irrational numbers, such as ? (pi), can also be expressed as rational numbers by using an infinite decimal expansion. For example:Īll decimal numbers can also be expressed as rational numbers. All whole numbers and integers are rational numbers, as they can be expressed as fractions with a denominator of 1. Rational numbers are any number that can be expressed as a fraction p/q, where p and q are integers and q is not equal to 0. Irrational numbers include ?2 (square root of 2, an algebraic number), ? (pi, a transcendental number), and Euler’s constant e. A real number that is not rational is called irrational. These statements hold true not just for base 10, but also for any other integer base b ? 2. Moreover, any repeating or terminating decimal represents a rational number. The decimal expansion of a rational number always either terminates after finitely many digits or begins to repeat the same finite sequence of digits over and over. The set of all rational numbers, often referred to as “the rationals”, is usually denoted by a boldface Q (or blackboard bold ?).
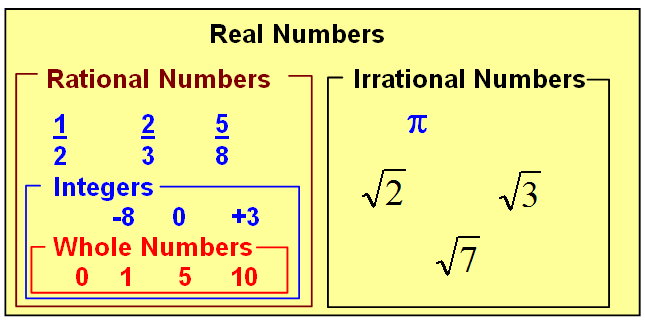
In mathematics, a rational number is any number that can be expressed as the quotient or fraction p/q of two integers, a numerator p and a non-zero denominator q. Rational Numbers Definitions and Examples


 0 kommentar(er)
0 kommentar(er)
